

Join me for a FREE, Guided Math workshop to discover how to easily incorporate Guided Math into your current schedule!
Second grade is a very important year when it comes to fact fluency. This is the time when they are learning to become familiar with two-digit addition and subtraction facts. In my previous post, I shared four addition strategies that I focus on Today, I’ll be sharing four subtraction strategies used for introducing 2 digit subtraction without regrouping.
Just like introducing 2-digit addition, I expose my students to multiple strategies and models they can use to solve subtraction problems. We spend lots of time focusing on WHY something is done before we teach HOW something is done. Giving students choice in their learning by providing them with multiple ways to solve problems is helping them succeed. Flexibility is key because every child learns differently.
The Texas TEK for two-digit subtraction states:
2.4B: Add up to four two-digit numbers and subtract two-digit numbers using mental strategies and algorithms based on place value and properties of operations.
The Common Core Standard for two-digit subtraction states:
2.NBT.B.5: Fluently add and subtract within 100 using strategies based on place value, properties of operations, and/or the relationship between addition and subtraction.
Note that the bolded text above says nothing about the standard algorithm we learned growing up years ago. Keep reading to learn about four subtraction strategies I introduce and teach my students when focusing on double digit subtraction without regrouping. Also, note that these strategies will not focus on regrouping. Students need a strong understanding of place value AND simple subtraction before moving onto that task.

At the beginning of our subtraction unit, I always make this subtraction without regrouping anchor chart. As we learn a new strategy, such as double digit subtraction without regrouping, it is added to our whole group chart. My students keep a matching copy of this in their math journals to use later on when they need extra support.


Before we get started, I want you to make sure you are familiar with the vocabulary that will be used.
Throughout this post, you will hear the terms minuend, subtrahend, and difference. In the problem 67-33=34, 67 is the minuend, 33 is the subtrahend, and 34 is the difference.
When introducing 2 digit subtraction without regrouping, I always start with the base ten models. In addition to using base ten blocks, I also teach them to draw the blocks out on paper. This is because students won’t always have access to manipulatives, but they will have a pencil and paper. I always give my students a place value mat placed inside a plastic sleeve. This allows students to also write or draw using a dry erase marker and they can be used over and over again. Here is how this strategy works using the example 59-15=44

For students to draw out this strategy it works the same way. We draw “sticks” to represent the tens and “dots” to represent the ones. I also teach them to take away or cross out the ones first followed by the tens. This will help when regrouping is introduced later on.

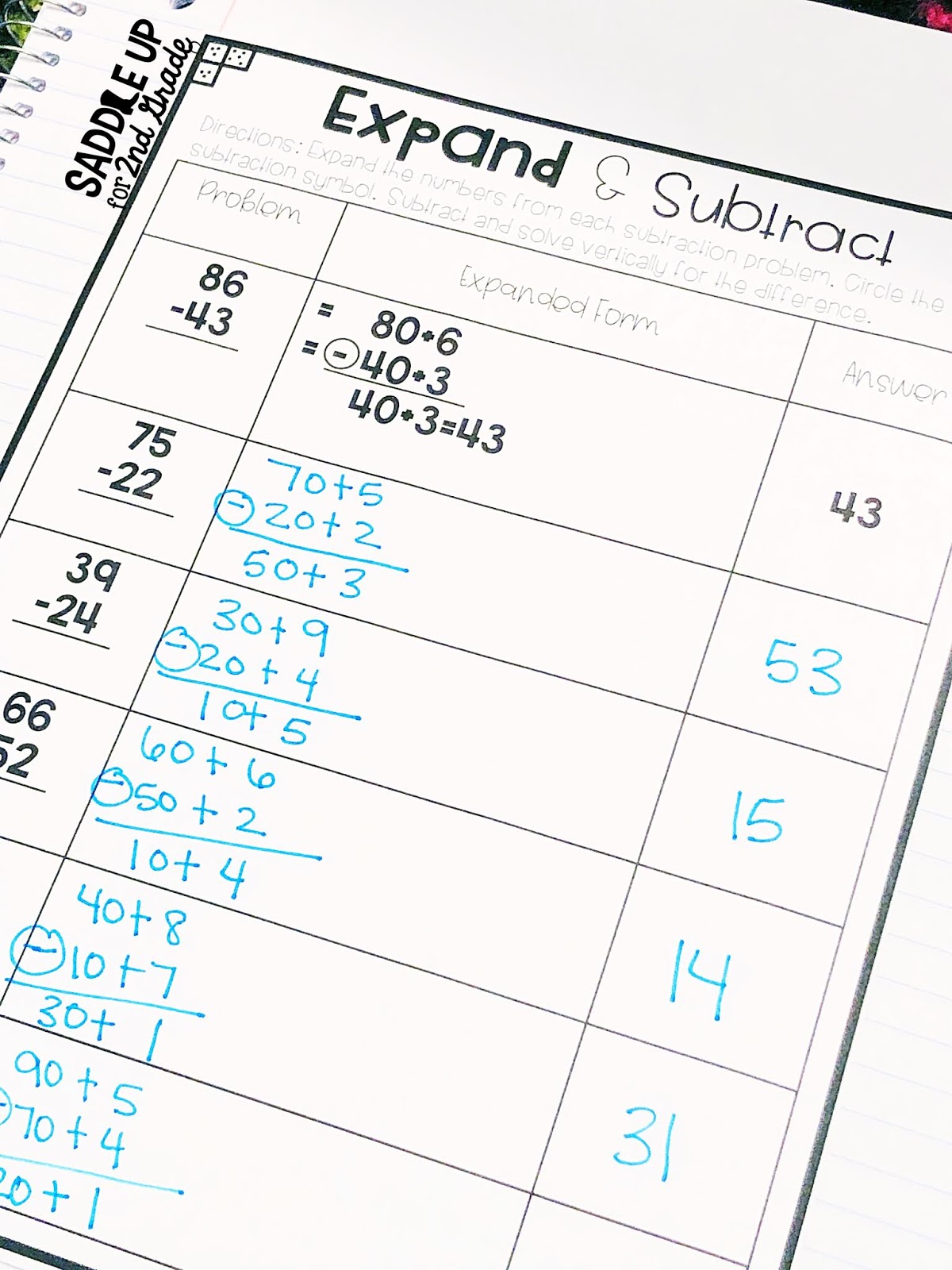
The second subtraction strategy that I introduce is the Expanded Form Method. Your students need a strong understanding of place value and expanding numbers for them to be successful using this strategy.
The minuend and subtrahend of the subtraction problem will be expanded and lined up vertically. I always have my students circle the minus sign to help them remember to subtract rather than add.
Here is how it works using the example 86-43.
Expand the minuend. >>> 80+6
Expand the subtrahend and write it vertically underneath the minuend. >>> 40+3
Circle the minus sign.
Subtract and solve vertically based on place value starting with the ones, then the tens.
Solve for the difference. >>> 40+3=43
The number line model subtraction strategy tends to be more challenging for students. They need a strong knowledge of mental math and skip counting for this method to come easily for them.
I often use skip counting as a warm-up for our math block. Example: Have students stand in a circle. Choose a student to go first and skip count by 10’s starting with the number 35. The first person says 35, the next says 45, and so on. For the ones that struggle I will often let them hold a hundred chart in their hand to help. You can have them do this counting forwards or backward.
Another way to squeeze in counting practice is to have them chant while they are lining up. Example: Class, let’s skip count by 2’s as we line up. We will start with the number 40 and see how high we can count. When everyone is lined up correctly, we will stop. The number line strategy focuses on students “hopping” and “skipping” backward on a number line to solve for the difference of a given problem. I call the 10’s hops, and the 1’s skips.
I’ve also found it helpful for students to write out their steps before solving the problem.
Here is how it works using the example 57-26.

This traditional method is probably how you learned two-digit subtraction growing up and is what our children’s parents are most familiar with.
For this strategy, students need to line up both numbers vertically underneath each other. The minuhend (larger number) goes on top and the subtrahend (smaller number) goes on the bottom. They will subtract the ones place first and then the tens place to solve for the difference.
One tip that can be helpful when first learning this strategy is to have students use a highlighter to highlight the ones place or have them circle the numbers in the ones place first. This helps them visualize where they need to start first. This concept can be more complicated for them than we realize because they are trained to read and write from left to right.

At the end of our unit, we always make these Subtraction Strategy Flipbooks to help us review. They can keep these to use later as a reference when needed.


Whew! That may seem like a lot of information to process.
We all learn concepts in different ways and the subtraction strategies that I have shared are what I have found to be beneficial for my own students. There is no right or wrong strategy when it comes to solving two-digit subtraction problems.
Allow your students to choose the method that works best for them and have them stick with it. Once they have found a method that they are comfortable with, it is important to provide them with multiple opportunities to practice.
Below are some resources that you may find helpful.
Addition and Subtraction without Regrouping Unit This unit features 10 days worth of hands-on and engaging activities for your students to practice all the subtraction strategies for double digit subtraction without regrouping that I have listed above. There are daily addition and subtraction word problems, interactive notebook prompts, subtraction without regrouping games and so much more.
Want to save these subtraction strategies ideas for later? Pin the image below!

Math should be fun, not stressful. Ditch the timed math fact tests and replace them with math games that will help your students learn and retain information more effectively.
© Saddle Up for 2nd Grade • Website by KristenDoyle.co